Mine planning is a big job. First there are long-term plans, then medium-term plans, and then short-term plans. The coordination and alignment of these different plans, typically by different people, requires significant effort. As we’ve seen, best practice dictates that longer term plans should drive shorter term plans, but how do we ensure that this occurs, and how do we assist planners in their processes?
Quantitative Measurement
When multiple people are involved, it is often useful to speak in quantitative terms; that is, we should measure things, rather than simply speak of “good” and “bad”. Once we have a quantitative measurement for something, it allows us to introduce concepts such as conformance standards. If a measurement is thoughtful, we can also use it to analyse issues of non-conformance, as well as compare results through improvements and other changes.
The Spatial Plan Alignment Index (SPAI)
The benefits of a quantitative measure are undeniable, but the typical measurement for plan alignment is a rather simplistic comparison of total tonnes per period. This “matching totals” approach doesn’t account for whether these are the “correct” tonnes. Mining the wrong tonnes can be just as detrimental to the plan as not mining at all.
One method for measuring plan alignment is the Spatial Plan Alignment Index (SPAI). It suggests that hierarchical planning should be applied not just chronologically, but also geospatially.
To calculate alignment, we need two plans: the shorter term plan and the longer term plan. SPAI starts with the idea that the alignment of a single block between these two plans may be calculated. Given the number of tonnes of a block mined in the shorter term plan (Sb) and the tonnes of a block mined in the longer term plan at or before the end of the shorter term plan (Lb), the Block Alignment Index (BAI) is calculated as:
$$BAI(b)=min(\frac{S_{b}}{L_{b}},1)$$
This BAI is a value ([0..1]) that describes the alignment of the shorter term and longer term plans for block b. For convenience, we will multiply BAI by 100 and view it as a percentage. The min() function ensures that additional tonnes in the short term plan will not result in an alignment greater than 100%.
By combining the BAI for all blocks in an area (B), we are able to calculate the SPAI of that area:
$$SPAI=\frac{\sum_{b \epsilon B}(BAI(b)\times L_b)}{\sum_{b \epsilon B}L_b}$$
This area could be a blast polygon, a bench, a pushback, or the entire mine. By combining all the blocks (weighted by tonnes), we obtain a measure of alignment of the area that isn’t just a comparison of total tonnes.
We can use a more detailed version of the BAI function BAI2 to ensure that we don’t take more tonnes from a block than planned:
$$BAI2(b)=\begin{cases}1-(\frac{|L_{b}-S_{b}|}{max(S_{b},L_{b})}) & max(S_{b},L_{b})\neq0\\1 & max(S_{b},L_{b})=0\end{cases}$$
We can then calculate a more accurate SPAI2 by weighting it with the larger of the short- or long- term tonnes:
$$SPAI2=\frac{\sum_{b \epsilon B}(BAI2(b)\times max(S_{b},L_{b}))}{\sum_{b \epsilon B}max(S_{b},L_{b})}$$
This alternate version is more complicated, but it helps avoid cases where the short term plan may be moving ahead of the longer term plan. While this might be viewed as acceptable for some materials (such as waste) it can actually have a detrimental effect on both value and sustainability, particularly if we require additional material to meet blending constraints later in the schedule.
Schedule Alignment
So far, we have considered the alignment of the plan as a whole. Often it is more useful to consider individual periods of a schedule. By calculating the SPAI for each period, we can see the alignment over the duration of the schedule.
Because the longer term schedule was created over longer time periods, we can assume that the longer term tonnes are uniformly divided into the shorter term plan’s equivalent periods. For example, a yearly longer term plan should have its tonnes for the first year divided by 4 and compared to the first four quarters of a quarterly shorter term plan.
In the case of extreme difference in time period size (such as yearly to monthly), we should not expect that the plans will align 100%. To account for this, we can use a cumulative SPAI. This can be calculated using the tonnes from the shorter and longer term plans up to and including the current period. By considering SPAI cumulatively, we allow the shorter term schedule to “catch up” to the longer term schedule.
Example
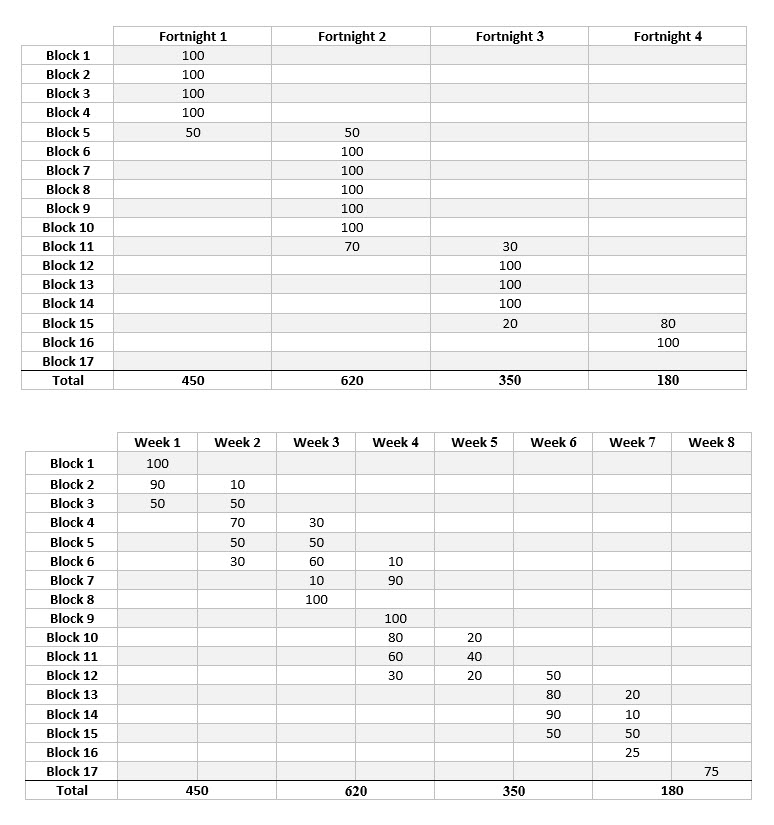
As a demonstration, let’s compare two simplified plans: a fortnightly plan and a weekly plan:
At first inspection, the weekly plan follows the fortnightly plan quite well. The total quantity in each fortnight of the weekly plan matches the fortnightly plan exactly.
Spatial analysis of the plan, however, notes that alignment isn’t perfect. The SPAI for the entire plan is 0.95. The more accurate SPAI2 is lower, at 0.91. These numbers would still imply a well-aligned shorter term schedule.
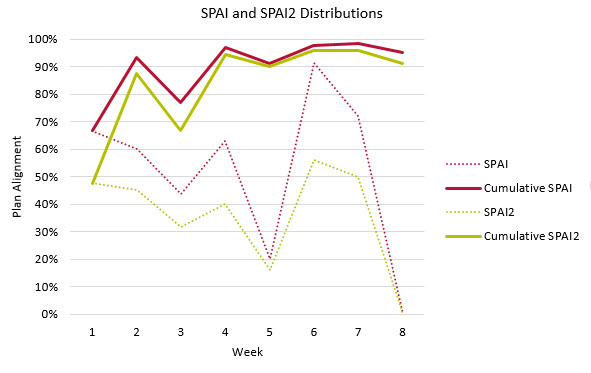
When calculating period-by-period SPAI, however, we see different results. Here we can see the SPAI and SPAI2, both purely period-by-period and also cumulatively:
Note that all measures show that the start of the plan is far from well-aligned. SPAI2 shows a decrease in alignment where additional material has been mined. While this might seem a bad result, when calculated cumulatively we can see that the weekly plan does quite a good job of catching up. The cumulative SPAI2 does drop in the final period, mostly due to the mining of Block 17 (which is not mined in the fortnightly plan).
Depending on the policies and goals of the organization, this alignment may not be satisfactory. We can use the SPAI values to direct us to the periods that are most in need of adjustment. By doing this, we ensure that the short term operation is directed toward the same optimal value of the longer term plan.
Conclusion
By using a spatial approach to comparing plans, we are able to quantitatively measure plan alignment. This allows us to unambiguously compare alternatives, set conformance standards, and analyse plans to make improvements. This, in turn, helps ensure that short-term planning is driving towards long-term optimized goals.
In our next article, we’ll discuss how plan alignment can be a driver for the optimization of your shorter term schedules. How do you compare your plan alignment? Do you have company-defined conformance standards? Let me know here.